| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
- 시간복잡도#기본산술연산#덧셈#곱셈#나눗셈#비트연산
- latent factor model
- Collaborative Filtering
- 협력필터링
- MLP
- Deep Learning
- neural network
- implicit feedback
- perceptron
- 알고리즘#수행시간#BigO
- 인공신경망 학습
- nn
- learning a neural network
- Universal Classifier
- parameters
- FCN #Fully Convolution #Semantic Segmentation
- tv shows
- Today
- Total
Study
Neural Networks Learning the network: Part 1 본문
This is a summary of Lecture 3 of 11-785 Deep learning at CMU.

'인공신경망은 universal function approximator이다' 라는 말의 뜻은, 만약 어떤 임의의 함수가 주어졌을 때, 인공신경망을 사용하여 주어진 함수를 임의의 정밀도로 근사하는 것(approximation with arbirary precision) 이 가능하다는 뜻이다.

음성인식이나 자동 캡션생성과 같은 문제는 입력이 주어졌을 때 입력에 대응되는 올바른 출력을 mapping해주어야 하는 문제이다. 따라서, 이 문제들은 입력과 출력을 mapping시키는 함수를 찾는 문제로 볼 수 있으며, 인공신경망은 어떤 함수든지 임의의 정밀도로 근사할 수 있기 때문에, 결과적으로 이 문제들은 출력이 결정적(deterministic)이라면 인공신경망을 사용해서 해결할 수 있다.

그렇다면 우리는 네트워크가 요구되어지는 기능을 제대로 잘 수행하도록 하기 위해서 어떻게 네트워크를 구성해야 할까?

퍼셉트론을 어떻게 작동하는지 무엇이 결정하는가? w_i와 b(weights와 bias)이다.
편향(bias)는 입력이 항상 1이고 가중치를 편향값과 동일하게 설정하는 방식으로 표현할 수 있다.

네트워크는 feed-forward이다.
Feed-forward: 계산은 방향을 따라 수행되며, 그 방향은 입력으로부터 시작해서 출력으로 향한다.
네트워크가 feed-forward라는 것은 네트워크에 입력이 주어졌을 때, 그 입력값들은 네트워크를 통과해서 출력을 만들어내며 그 과정에서 네트워크의 퍼셉트론(=뉴런)들은 한번 방문되었다면 재방문되지 않음을 의미한다.
네트워크는 총 몇개의 퍼셉트론으로 구성되어있으며, 네트워크는 몇개의 은닉층으로 구성되어있는지, 또는 네트워크 내부에서 퍼셉트론끼리 어떻게 연결되어 있는지 등을 표현하는 네트워크의 디자인을 네트워크 아키텍쳐(architecture)라고 부른다.
앞으로 우리는 네트워크의 아키텍쳐는 우리가 원하는 함수를 표현하기에 충분한 능력(capacity) 또는 크기를 가지고 있다고 가정하고 나머지 주제를 다루고자 한다.
여기서 네트워크의 아키텍쳐가 충분한 크기를 가진다는 의미는 네트워크의 너비와 깊이가 목표 함수를 표현하기에 충분히 크다는 것을 말한다.

네트워크를 구성하는 가중치들의 집합을 $W$라고 하고 입력을 $X$라고 하면, 네트워크는 입력 $X$를 출력 $Y$에 mapping하는 하나의 함수로 여길 수 있다.
이 함수를 $f(X;W)$라고 표기했을 때, 세미콜론 뒤에 오는 $W$는 함수의 파라미터를 나타내며, 이 파라미터의 값이 함수가 어떻게 동작할지 결정한다.
따라서, 인공신경망을 학습시킨다는 것(learning a neural network)은 인공신경망으로 하여금 우리가 원하는 함수를 표현하게 하기 위해서 네트워크를 구성하고 있는 파라미터의 값을 적절한 값으로 결정하는 것을 의미한다.
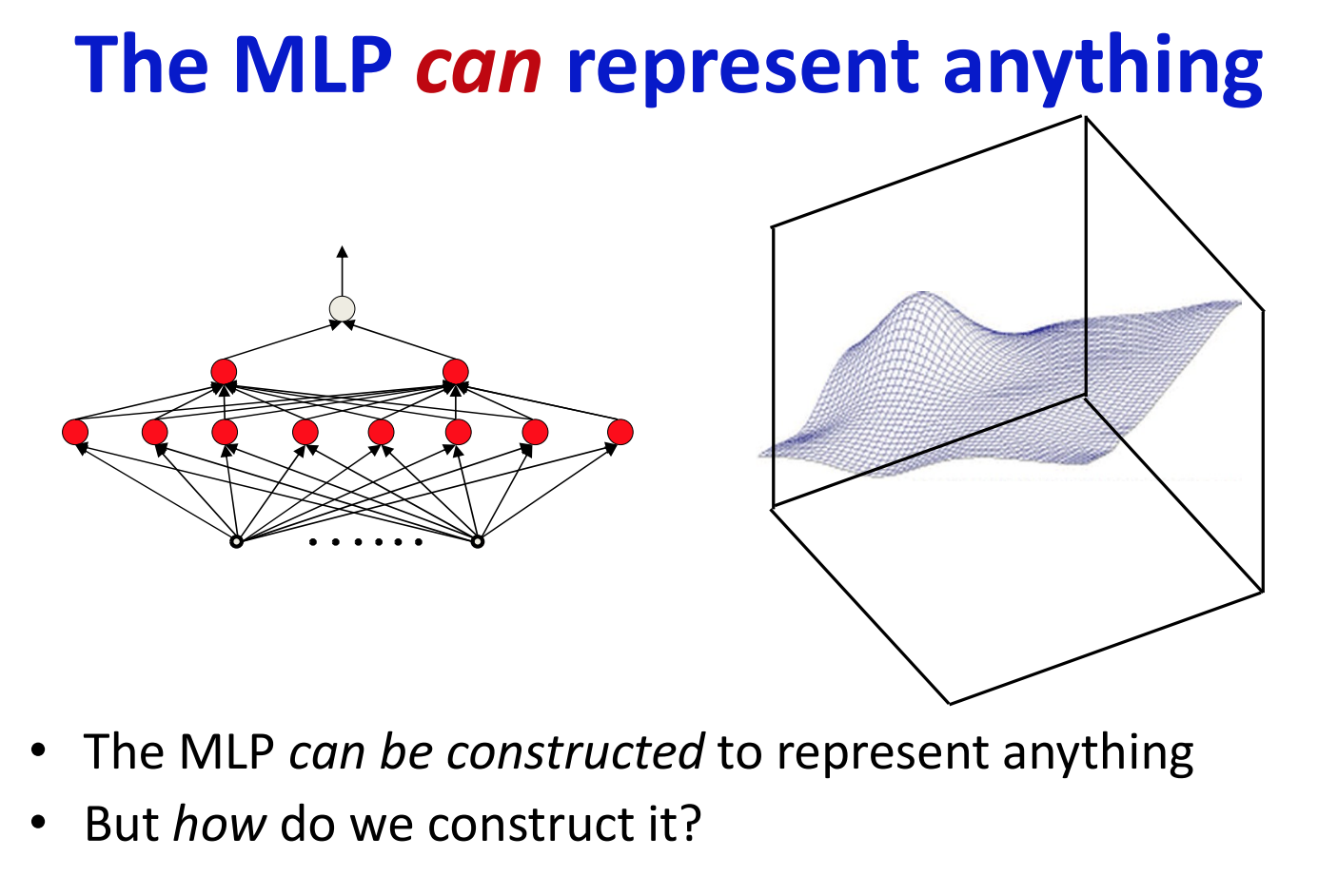
우리는 MLP가 어떠한 함수든 다 표현할 수 있는 것을 알고 있다. 그렇지만 어떻게 MLP로 하여금 원하는 함수를 표현하도록 만들 수 있을까?
오른쪽의 매쉬로 표현되어있는 3차원의 등고선을 MLP로 표현하고자 한다고 가정해보자.

위의 예시처럼 복잡한 3차원 매쉬로 표현된 함수를 살펴보기 이전에, 간단한 결정경계를 갖는 함수부터 살펴보자.
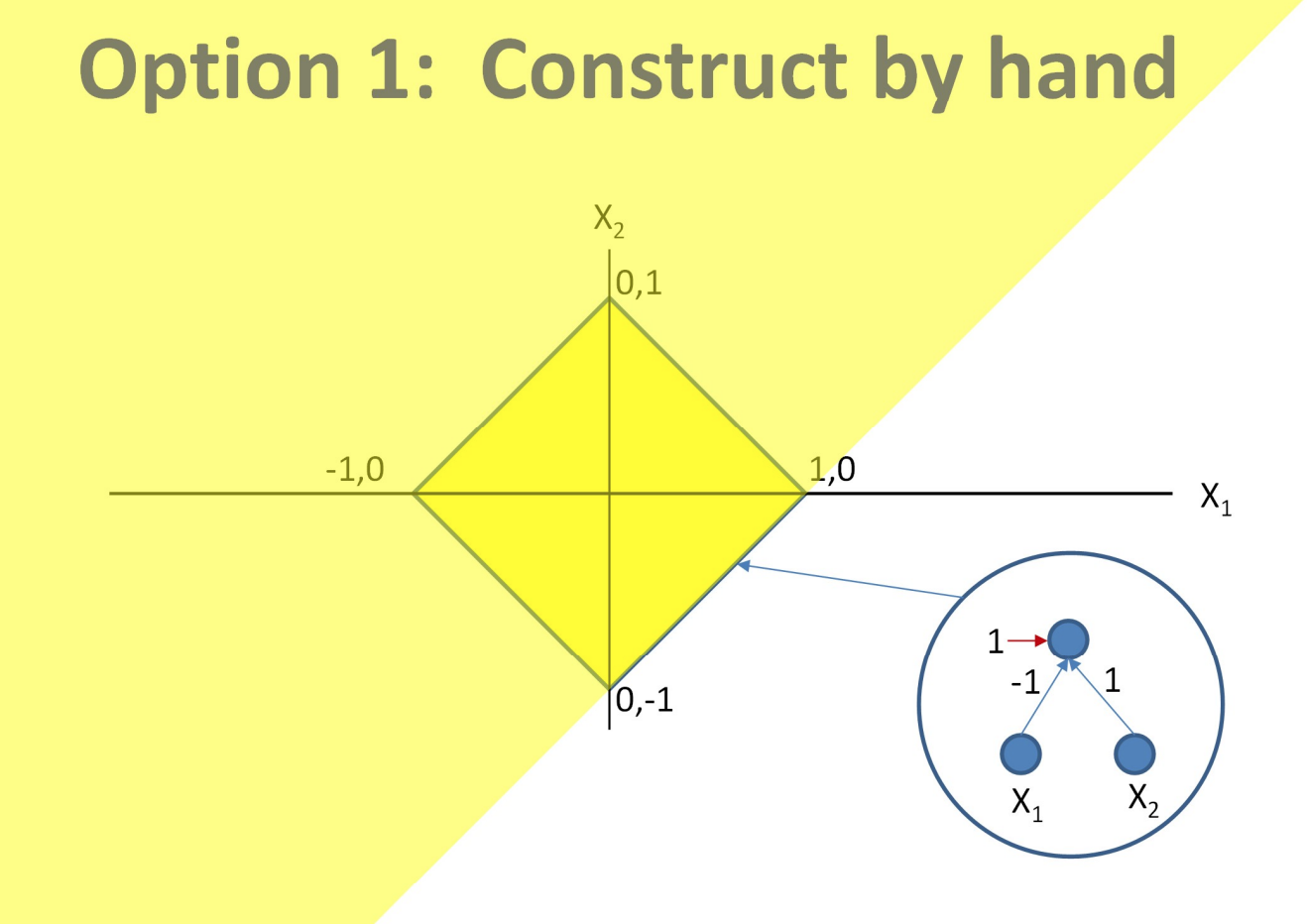
왼쪽의 노란 마름모 모양의 결정경계를 표현해야 하는 경우는 충분히 간단하기 때문에 사람이 직접 계산하여 그 결정경계를 찾을 수 있다.
아래의 표는 마름모 결정경계의 네 변에 대응되는 퍼셉트론들과 그 가중치를 구하는 과정을 나타내고 있다.
 |
 |
 |
 |
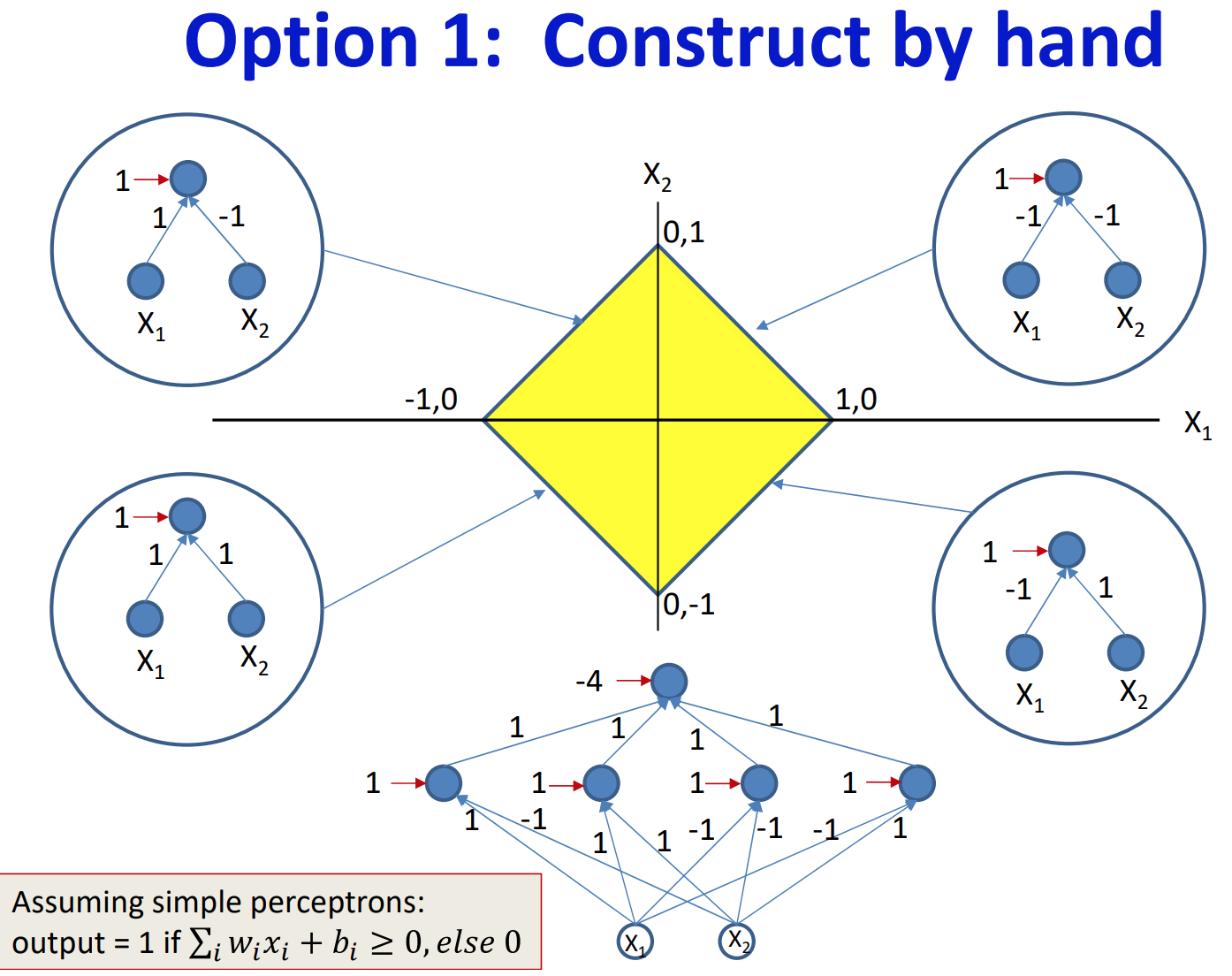
위의 과정을 통해 결정경계의 각 변을 나타내는 퍼셉트론을 하나씩 생성한 후에 이들을 and게이트로 묶음으로써 마름모 형태의 결정경계를 갖는 함수를 표현하는 네트워크를 우리가 직접 찾아낼 수 있다.
하지만 이는 결정경계가 매우 단순하기에 가능한 일이며, 결정경계가 복잡해지면 사람이 절대로 직접 계산하여 네트워크를 디자인할 수 없다.
따라서 우리가 원하는 것은 원하는 함수를 표현하기 위한 네트워크의 파라미터를 네트워크 스스로가 학습하는 것이다.

우리가 모방하고자 하는 함수가 $g(X)$라고 해보자.
그러면 우리가 원하는 것은 $f(X;W)$가 $g(X)$와 유사하게 동작하도록 파라미터 $W$의 값을 결정하는 것이다.

설명의 단순화를 위해(2차원 그래프로 표현하기 위해서), 잠시 $X$가 스칼라값을 가진다고 가정해보자.
왼쪽의 그래프에서 우리가 모방하고 싶은 함수 $g(X)$가 파란 점으로 표현된 곡선이고, 빨간 점으로 표현된 곡선이 현재 설정된 $W$의 값에 의해 묘사된 함수 $f(X;W)$라고 해보자. 이 상황에서 우리는 두 함수 $g(X)$와 $f(X;W)$ 사이의 차이를 최소화 하기 위해서 $W$값을 조정하고 싶다. 두 함수의 차이를 최소화한다는 것은, 왼쪽의 그래프에서 파란 점으로 표현된 곡선과 빨간 점으로 표현된 곡선 사이에 음영표시된 영역을 최소화 하는 것을 의미한다.
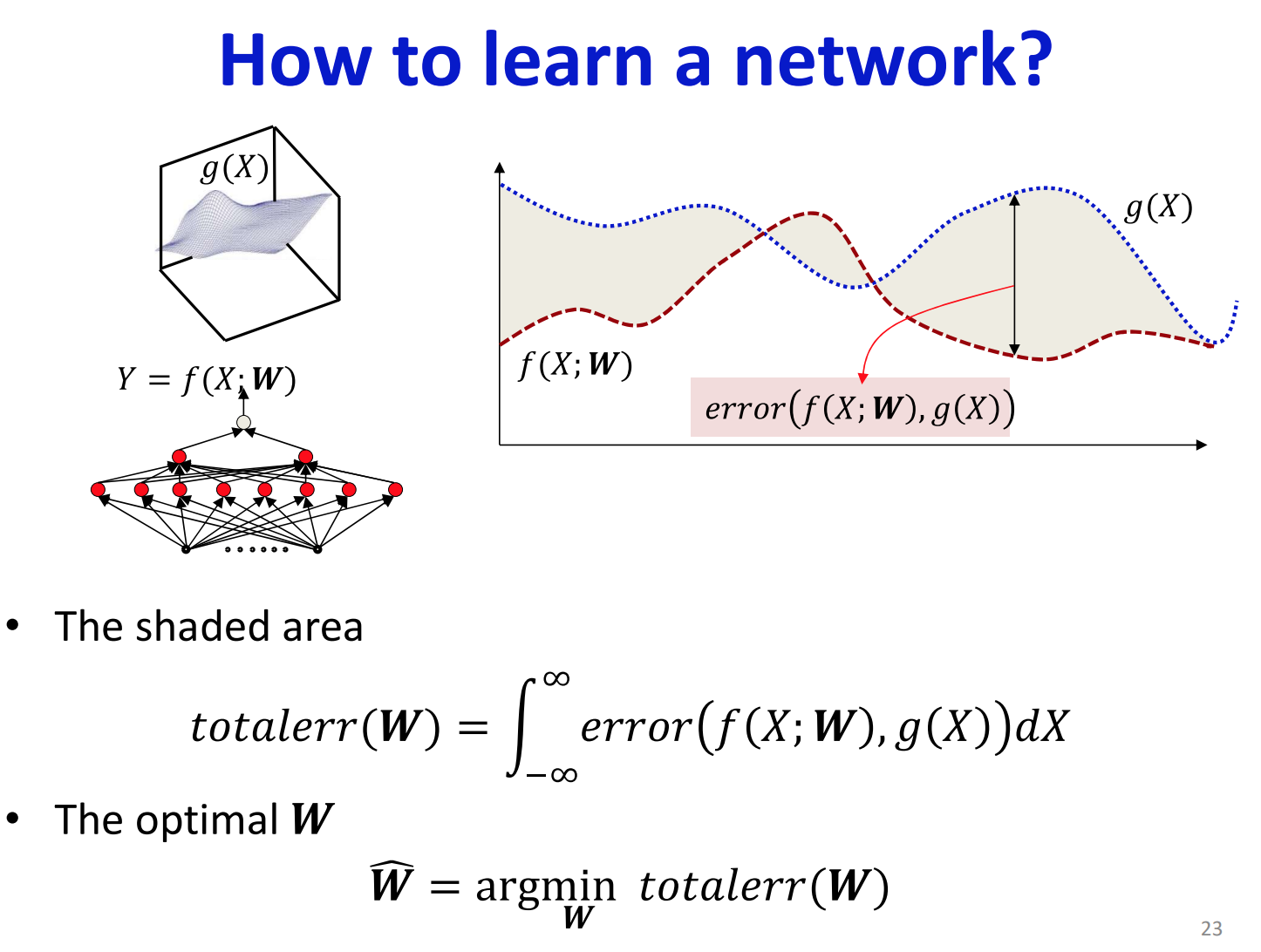
그렇다면 음영 영역을 최소화하기위해서 필요한 것은 무엇인가?
해당 영역의 면적이 얼마나 넓은지를 계산할 수 있어야 한다. 즉, 두 함수 사이의 양적 차이를 수치화 할 수 있어야 한다.
그러기 위해서 $X$가 임의의 값을 가질 때, $f(X;W)$와 $g(X)$가 해당 값을 입력으로 받아서 출력한 값들의 차이를 error라고 하면, error를 $X$가 가질 수 있는 모든 값들에 대하여 적분한 것이 음영영역의 면적이다.
그런데 이 error를 계산할 수 있으려면 우리가 이미 $g(X)$를 알고있다는 가정이 필요하다. 하지만 현실에서 이 가정은 만족되지 못하는 경우가 대부분이다. 그리고 이미 우리가 $g(X)$를 알고 있다면 굳이 인공신경망을 통해서 $g(X)$를 근사할 필요가 왜 있겠는가?
그렇다면 $g(X)$를 모르는데 어떻게 error를 계산할 수 있을까?

최대한 서로 다른 입력에 대한 $g(X)$ 값을 샘플링함으로써 문제를 해결한다.
이는 우리가 $g(X)$를 알고있다는 뜻이 아니라, 우리가 몇몇의 특정 입력 $X_i$ 에 대한 $g(X_i)$ 값을 알고있다는 것을 의미한다.
따라서, 우리는 보통 학습데이터를 많이 수집함으로써 샘플의 수를 늘리고자 한다.

어쨌든, 우리가 원하는 것은 주어진 샘플들을 가지고 네트워크가 함수 $g(X)$ 전체를 정확하게 표현할 수 있도록 학습시키는 것이다.

우리는 모든 정의역에 대한 $g(X)$값을 아는 대신에 일부 입력에 대한 값만 아는 상태이다.
우리가 입력 $X_1$, $X_2$, $X_3$, $X_4$, $X_5$에 대한 $g(X_i)$ 값을 알고 있다고 가정해보자.
그러면 우리가 할 수 있는 일은 $X_i$(where $i=1, ..., 5$)에 대한 empirical error를 계산하고 이를 최소화 하는 것이다.
empirical error라고 부르는 이유는, 함수 전체가 아닌 일부 샘플에 대해서만 error를 계산하기 때문이다.
샘플에 대한 empirical error를 계산하고 이를 최소화하는 $W$를 찾았을 때, 그때의 $W$가 $g(X)$와 $f(X;W)$를 정의역 전체에 대해서도 error를 최소화하는 $W$ 이기를 바라면서 $W$를 찾는 것이다.

이러한 관점에서 네트워크를 학습시키는 문제를 다시 한번 표현해보자면, 학습이란 우리가 이미 알고있는 샘플에 대하여 네트워크의 출력과 실제$g(X)$의 값의 차이를 최소화하는 네트워크 파라미터를 찾음으로써 네트워크가 정의역 전체에 대하여 함수 $g(X)$를 잘 근사하도록 만드는 것이라고 할 수 있다.

지금까지의 내용을 정리해보자면,
'네트워크 학습'이란 네트워크가 원하는 목표 함수를 모델링하기 위해 요구되어지는 네트워크의 파라미터 값들을 결정하는 일이다.
그리고 우리는 학습시킨 네트워크가 목표 함수를 모든 정의역에 대하여 제대로 잘 표현하길 바라는데, 애초에 목표함수를 정확하게 안다는 것이 불가능하다. 따라서, $g(X)$로부터 샘플링하여 구한 '입력-출력' 쌍의 학습데이터들을 가지고 최대한 이 샘플들에 대한 네트워크의 출력과 $g(X)$값이 유사해지도록 만듦으로써 이를 달성하고자 한다.

먼저 제일 단순한 이진분류문제에 대하여 살펴보고자 한다. 그러기 위해서 입력이 스칼라값일 때 출력이 0 또는 1인 함수를 근사하는 경우를 생각해보자.
왼쪽의 그래프에서 파란 점선이 입력 $X_i$에 대한 원하는 출력을 표현하고 있고, 빨간 실선이 실제로 네트워크가 입력에대해 만들어낸 출력을 표현하고 있다고 해보자. 이 예시에서 우리의 네트워크는 현재 $X_3$과 $X_4$에 대하여 즉 2개의 샘플에 대하여 오분류하고 있는 상황이다.
이 때 우리가 원하는 것은 $W$ 값을 조정함으로써 네트워크가 오분류하는 샘플의 수를 최소화하는 것이다.

우리가 원하는 것이 빨간색으로 표현된 3차원의 step function이라고 하고, 실제로 우리가 알고 있는 것은 파란 점들과 빨간 점들로 표현된 샘플들이라고 해보자.
그렇다면 우리는 이미 알고 있는 샘플들만 가지고 이 step function을 올바르게 표현하는 $W$를 알아내야 한다.

그러한 $W$($W$는 $w_i$들과 $b$를 포함)는 빨간 점들로 표현된 샘플들에 대해서는 네트워크의 출력이 0보다 크도록하고, 파란 점들로 표현된 샘플들에 대해서는 네트워크의 출력이 0보다 작거나 같도록 하는 파라미터이다.

퍼셉트론을 $N$차원의 입력에 대한 affine 연산으로 보는 대신에,
실제 입력 외에 추가로 가상의 입력으로 1을 받고, 1에 대한 가중치를 $b$로 설정함으로써
$N$ 차원의 원점을 지나지 않는 평면 대신에,
$N+1$차원의 원점을 지나는 평면으로 표현할 수 있다.

그러면 우리가 풀고자하는 문제는,
2차원의 빨간 점들과 파란 점들이 샘플로 주어졌을때
주어진 점들을 잘 분리하면서 원점을 지나는 3차원상의 초평면(hyperplane)을 찾는 것으로 바뀌게 된다.

설명의 편의를 위해서 네트워크의 입력과 가중치들을 벡터로 표현하면, 입력벡터 $X=[X_1, X_2, ..., X_N, 1]$ 와 가중치벡터 $W=[w_1, w_2, ... w_N, w+{N+1}]$ 로 표현된다. 벡터들로 원점을 지나는 초평면을 표기해보면 $W^TX=0$라고 할 수 있는데, 이 식을 만족하는 벡터 $W$는 벡터 $X$에 수직이다.(두 벡터의 내적 값이 0이므로)
만약에 우리가 모은 샘플들이 다 빨간 점들로 표현된다면, 이 빨간 샘플들에 대한 $W^TX$ 값은 양수여야 한다. 이를 만족시키는 $W$ 중에서 가장 구하기 쉬운 $W$는 $X$에 양의 상수를 곱한 벡터($W=aX$, where $a>0$)일 것이다. 이는 벡터 $W$의 방향이 빨간 샘플들을 나타내는 벡터들의 방향과 동일함을 의미한다.

반대로, 파란 점들로 표현된 샘플에 대해서는 $W^TX$ 값이 음의 값이어야 하므로, 벡터 $W$가 파란 점들을 나타내는 입력벡터들과는 반대방향을 향해야 한다.
이미 모든 샘플들을 알고 있다면 위와 같은 방식으로 closed form solution을 계산할 수 있다. (*closed form solution이란, 닫힌 형태를 가지는 방정식의 해로, 변수(variable), 상수(constant), 사칙연산( +−×÷), 그리고 잘 알려진 기본 함수(삼각함수, 로그함수, 제곱근 등) 등을 조합해서 “해 = …” 꼴로 표현할 수 있는 것을 말한다.)

하지만 Rosenblatt이 처음에 퍼셉트론의 개념에 대하여 발표했을 때, 퍼셉트론은 online으로 학습하도록 설계되었다.
online으로 학습한다는 의미는, 네트워크의 파라미터인 $W$ 가 초기에는 임의로 그 값이 정해진 상태에서 입력이 주어질 때마다 설정된 $W$ 를 이용하여 출력을 계산한 뒤, 그 출력이 원하는 값과 다를 때마다 $W$ 를 업데이트하는 방식을 말한다.

맨 처음 $W$ 를 초기화한 뒤에, 전체 학습 데이터에 대하여 하나씩 네트워크의 입력으로 삼아 출력을 계산하고, 그 출력이 잘못된 데이터만 $W$ 를 업데이트하는 데에 사용된다.
입력 데이터 $X_i$ 에 대하여 원래 기대되어지는 출력 값이 양의 클래스였는데 음의 클래스로 출력된 경우, $W$ 에 $X_i$ 를 더해줌으로써 $W$ 가 $X_i$ 의 방향으로 향하도록 업데이트 해준다. 반대로, 입력 데이터 $X_i$ 에 대하여 원래 기대되어지는 출력 값이 음의 클래스였는데 양의 클래스로 출력된 경우, $W$ 에 $X_i$ 를 빼줌으로써 $W$ 가 $X_i$ 의 반대방향으로 향하도록 업데이트 해준다.

학습데이터의 레이블 $y_i$ 가 0 또는 1이 아니라 -1 또는 1 의 값을 갖는다고 하면 조금 더 간편하게 $W$ 가 업데이트되는 과정을 기술할 수 있다.
처음에 $W$를 초기화하고, 모든 학습데이터에 대하여 한 바퀴 돌면서$W^TX_i$의 부호를 계산한 뒤, 그 부호가 $X_i$의 레이블인 $y_i$와 동일하지 않으면 $W$ 에 $y_{i}X_{i}$를 더하여 업데이트 해준다.
$X_i$가 오분류되는 경우를 생각해보면, $W^TX_i$가 원래 기대되어지는 $y_i$의 값과는 반대의 값($y_i=-1$이지만 $W^TX>0$인 경우와 $y_i=1$이지만 $W^TX<0$인 경우)을 갖게 된다.
- $y_i=-1$ 이지만 $W^TX>0$인 경우, $y_{i}X_{i}= -X_{i}$가 되어 $W$에 $y_{i}X_{i}$를 더하면 $W$에 $X_i$를 빼는 것과 동일하다
- 반대로, $y_i=1$이지만 $W^TX<0$ 인 경우, $y_{i}X_{i}= X_{i}$가 되어 $W$에 $y_{i}X_{i}$를 더하면 $W$에 $X_i$를 더하는 것과 동일하다.
따라서 $W^TX_i$의 부호가 $X_i$의 레이블인 $y_i$와 동일하지 않으면 $W$에 $y_{i}X_{i}$ 를 더하여 업데이트할 수 있다.

이를 그림으로 나타내면 다음과 같다.
먼저 $W$를 랜덤으로 초기화 한뒤, $W$로 주어진 데이터에 대하여 분류를 해본다.
당연히 랜덤으로 설정한 $W$는 데이터를 잘못 분류하기도 한다.

만약 원래 -1 클래스(blue)에 속하는 데이터가 1 클래스(red)로 잘못 분류된 경우, 해당 데이터를 $W$ 벡터에서 뺀다.

그러면 $W$가 새롭게 업데이트 된다.

새롭게 업데이트된 $W$로 인해 결정경계도 새롭게 업데이트 되었다.

이번에는 1 클래스(red)에 속한 데이터를 -1 클래스(blue)로 잘못 분류한 경우이다.

이 경우, 잘못 분류된 데이터를 $W$ 벡터에 더한다.

그러면 $W$가 새롭게 업데이트 되고,

결경경계도 새롭게 업데이트된다.
만약 데이터가 선형분류가 가능하다면, 유한한 횟수 안에 해당 알고리즘은 수렴한다.

선형분류가 가능한 경우,
$R$이 원점으로부터 가장 먼 데이터 포인트의 원점으로부터의 거리(norm)이고
$\gamma$가 잘 분류되었을 때 결정경계와 가장 가까운 데이터 포인트의 결정경계로부터의 거리일 때(SVM에서의 margin),
Perceptron algorithm은 $(\frac{R}{\gamma})^2$안에 수렴한다.
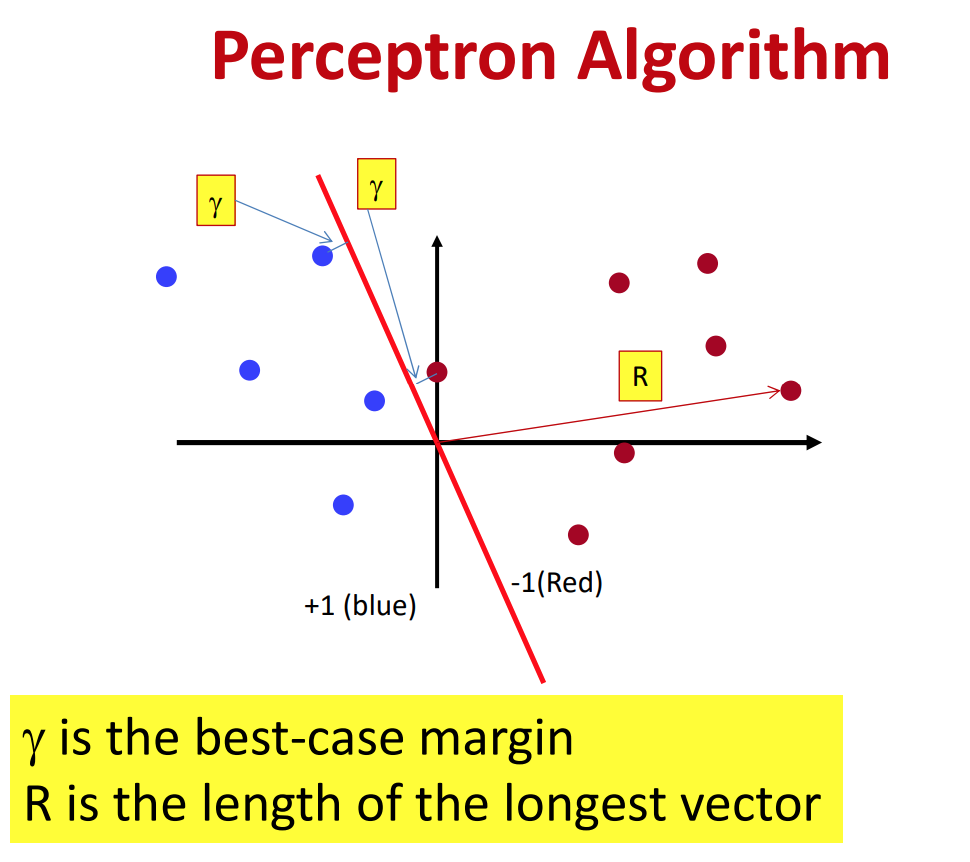
$R$과 $\gamma$는 왼쪽 그림에서 표현된 것처럼 정의된다.

그렇다면 데이터가 선형으로 분류되지 못하는 경우는 어떻게 될까?

알고리즘은 수렴하지 못하고 끊임없이 $W$를 재계산하게 된다.

앞에서 우리는 MLP를 통해서
충분한 개수의 퍼셉트론을 사용한다(모델의 capacity가 충분하다)는 가정 하에 왼쪽의 여러개의 다각형으로 구성되어있는 결정경계를 표현할 수 있음을 살펴보았다.
만약 우리가 그러한 MLP 구조를 이미 알고있다고 해보자.
그렇다고 하더라도 그 MLP를 왼쪽의 결정경계를 학습하도록 만들려면 어떻게 해야할까?

가장 낮은 레벨(입력층과 가까운 레벨)의 퍼셉트론들은 선형분류기이다.
그런데 해당 퍼셉트론에게 제공되는 데이터의 레이블들은 선형으로 분류가 불가능한 상태이다.
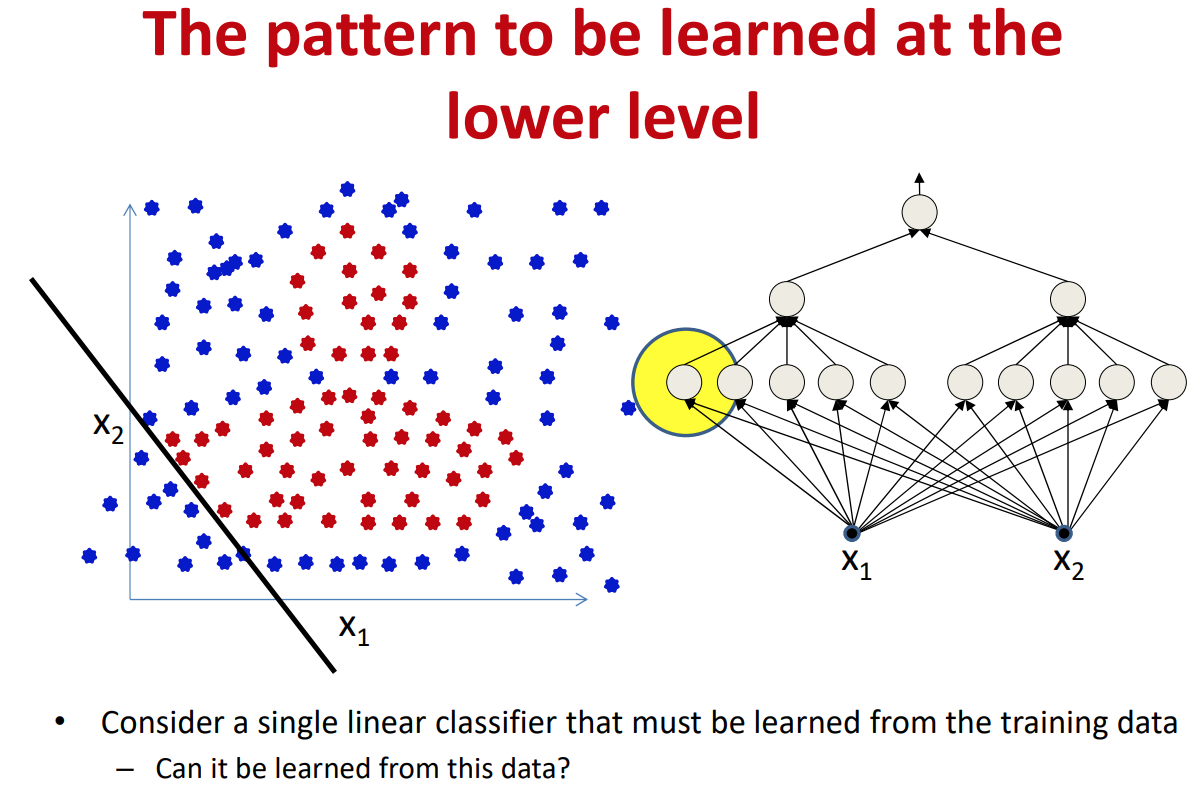
만약 전체 MLP중에서 딱 한개의 퍼셉트론만 잘 학습시키면 전체 MLP가 제대로 동작한다고 가정해보자.
그리고 그 한개의 퍼셉트론이 왼쪽 그림에서 노란색 원으로 표시된 퍼셉트론이고, 그 퍼셉트론이 학습해야 하는 선형 결정경계가 $x_1$, $x_2$평면에 표시되어있다고 해보자.

그럼 이 퍼셉트론이 올바른 선형 결정경계를 학습하기 위해서 필요로 하는 데이터의 레이블은 왼쪽의 그림과 같다.
(결정경계의 한 쪽에 위치한 데이터들은 동일한 하나의 레이블(예:blue)을 가지고, 반대쪽이 또 다른 레이블(예:red)을 가지도록 설정되어 있어야 함)

지금은 낮은 레벨의 퍼셉트론 한 개만 살펴봤지만,
사실 MLP 전체가 제대로 동작하려면 낮은 레벨에 속한 퍼셉트론 각자가 모두 제대로 학습되기에 알맞도록 다시 레이블된 데이터들이 제공되어야 한다.

그러러면
일단 하나의 선형 결정경계에 대해서만 생각해봐도,
각 데이터가 2개의 클래스 중 하나에 속하는 모든 경우의 수를 생각해보면 $2^{#.data}$ 이다.

그런데 하나의 결정경계가 아니라 모든 낮은 레벨에 속한 퍼셉트론에 대해서 동일한 행위를 반복해야하고,
낮은 레벨의 퍼셉트론으로부터 넘어온 정보는 다시 더 높은 레벨의셉트론에 의해 조합되어 우리가 원하는 패턴을 만들어내는데 활용된다.
그러기 위해서 우리는 입력 데이터에 대해서 지수(exponential) 횟수번 만큼의 탐색을 반복해야한다.

그런데다가 전체 네트워크의 입력과 출력에 대해서만 데이터가 수집되어 있기 때문에,
우리는 중간 뉴런들에게 적절한 출력이 무엇인지는 알지도 못한다.

이러한 문제가 발생하는 원인은 이진분류 결과로는 우리가 알 수 있는 정보가 많지 않기 때문이다. 예를 들어 왼쪽의 그래프에서
우리가 원하는 것은 파란 점선의 분류기이고(정답),
실제 우리의 분류기는 빨간 실선처럼 동작한다고 가정해보자.
그렇다면, 우리가 결정경계를 살짝 왼쪽이나 오른쪽으로 움직인다고 하더라도 이진분류의 오류는 변하지 않는다.

왼쪽의 퍼셉트론의 경우도 동일하다.
우리가 결정경계를 원점을 기준으로 살짝 오른쪽 혹은 왼쪽으로 회전시킨다고 하더라도 오류는 줄어들지 않는다.
따라서, $W$를 어느 방향으로 업데이트 시켜야 하는지에 대한 힌트를 전혀 받을 수 없다.

마찬가지로 MLP안에 속한 각각의 퍼셉트론의 파라미터들은 전체 오류 값을 변화시키지 않으면서 변할 수 있다.

그런데다가 우리가 다루는 데이터는 그다지 깔끔하지도 않아서
선형으로 분류될 수 있는 데이터는 그렇게 많지 않다.

먼저 결정 경계를 살짝 수정함으로써 잘못 분류되었다고 판단하는 방식을 바꿔서, 우리가 결정경계를 살짝 움직였을때 그 방향이 올바른 방향인지 아닌지 판단할 수 있도록 해야한다.
그러기 위해서는 퍼셉트론의 activation 함수를 변경시켜야 하고, 또 잘못 분류되었다고 평가하는 방식을 변경시켜야 한다.

acitvation 함수의 도함수가 입력이 포함되는 대부분의 영역에 대하여 0이 되지 않도록 step 함수가 아닌 다른 미분 가능한 함수로 변경한다.
그렇게 되면, 파라미터 값을 조금만 바꿔도 출력의 결과에 무시하지 못할 변화가 생기게 된다.

예를 들어 activation 함수를 step 함수에서 sigmoid함수로 변경하는 경우, 결정경계가 조금만 왼쪽 혹은 오른쪽으로 이동하더라도 실제 데이터로부터 activation 함수까지의 거리는 달라진다.
비록, 이진분류 오류가 달라지진 않더라도 거리값이 달라지기 때문에 이를 proxy삼아서 올바른 방향으로 $W$를 업데이트 해나갈수 있게 된다.


미분가능한 activation 함수를 사용하면 퍼셉트론의 출력도 퍼셉트론의 입력 $x_i$와 가중치 $w_i$에 대하여 미분 가능해진다.
그렇게 되면, 우리는 입력이나 가중치의 작은 변화에 대하여 퍼셉트론의 출력이 어떻게 변화하는지 알 수 있게 된다.
어떻게 네트워크를 학습시킬 수 있을까?
네트워크의 출력 $f(X;W)$와 실제 목표로 하는 함수 $g(X)$사이의 차이를 계산하는 divergence 함수를 정의해야 한다.
Divergence 함수는 두 함수의 출력값이 같으면 0, 그렇지 않으면 0보다 큰 값을 반환하는 함수로, 네트워크의 출력과 목표로하는 함수 사이의 차이가 얼마나 큰지 측량하는 함수이다.
Divergence 함수도 미분 가능하면, 입력 또는 각 퍼셉트론의 파라미터값 변화에 따른 네트워크 출력의 변화를 알 수 있게 된다.

이를 확장하면, 네트워크를 구성하고 있는 모든 함수가 모든 파라미터에 대하여 미분가능하다라고 할 수 있다.
그렇게 되면 우리는 파라미터상의 작은 변화가 어떻게 네트워크의 출력을 변화시키는 지 알 수 있게 된다.
(나중에 chain rule을 활용해서 정확한 도함수를 계산할 수 있다.)

학습데이터셋의 입력-출력의 쌍이 $(X_1, d_1), (X_2, d_2), ..., (X_N, d_N)$ 이라고 해보자.
그러면 $d$는 입력 $X$에 대응돼서 네트워크가 출력하길 바라는 값이다.
우리는 네트워크가 각각의 입력에 대응되는 바라는 출력값을 생성하도록 만들기 위해서 적절한 네트워크의 파라미터를 찾아야한다. (이때, 네트워크 구조는 이미 파라미터만 제대로 찾으면 원하는 대로 동작할 수 있도록 올바른 크기로 설정되어 있다고 가정.)
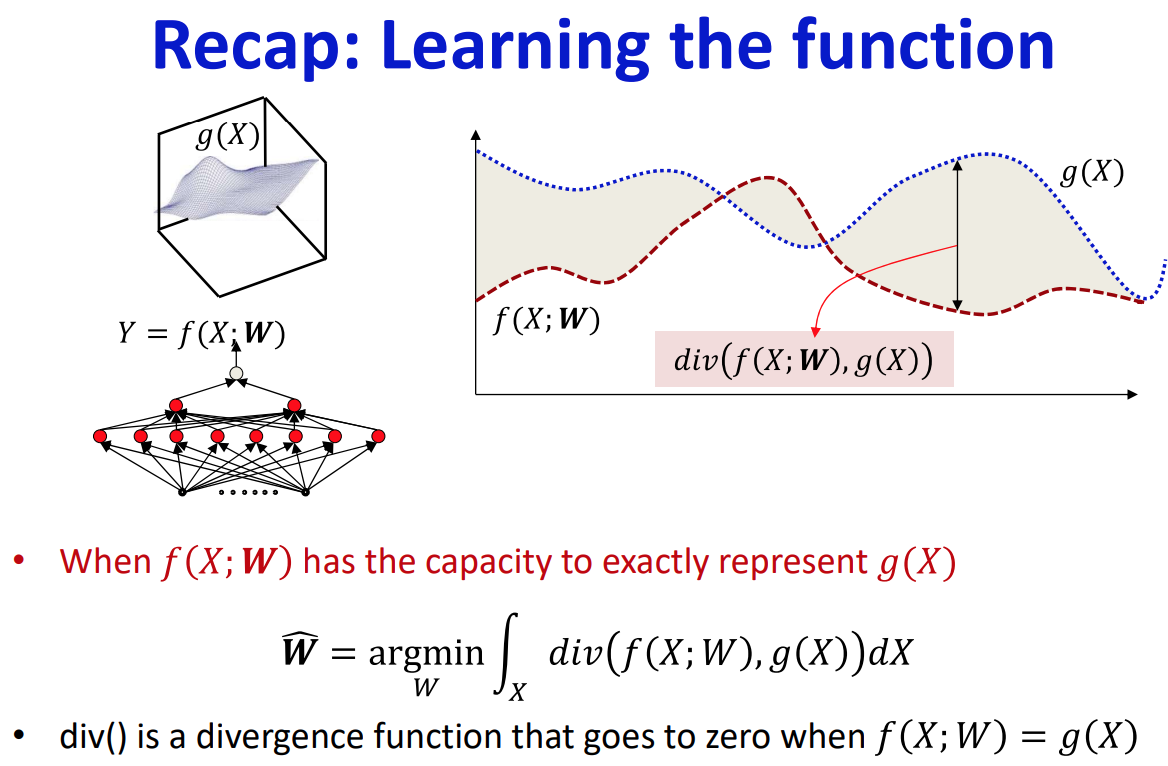
다시 리마인드 하자면,
만약 네트워크 $f(X;W)$가 목표 함수 $g(X)$를 근사하기에 충분한 크기를 가지고 있다면,
최적의 $W$는 모든 정의역의 범위에서 $div(f(X;W), g(X))$값을 적분했을 때 그 값을 최소로 하는 $W$이다.

그리고, 더 일반적으로 $X$를 랜덤변수로 가정하면
$X$의 정의역에 대하여 $div(f(X;W), g(X))$를 적분한 값을 최소화하는 $W$를 $\hat{W}$라고 했을 때 $\hat{W}$은 일반화 오류(generalization error)인 $div(f(X;W), g(X))$의 기댓값을 최소화하는 $W$이다.

그런데 우리는 $g(x)$를 알 수 없고,
단지 $g(X)$로 부터 뽑힌 샘플들만 알고 있다.
그렇기 때문에 샘플들로부터 $g(X)$를 유추해야 한다.

그리고 expected divergence는 입력이 이루는 전체 영역에 대한 평균 divergence값이다.
그리고 expected divergence의 경험적 추정은 샘플로부터 계산한 평균 divergence이다.

전체 학습데이터에 대하여 계산한 경험적 average divergence를 Loss라고 부른다.
그리고 expected divergence의 경험적 추정치를 최소화하는 파라미터를 $\hat{W} = \argmin_w Loss(W)$라고 한다.
expected divergence의 경험적 추정치는 각 데이터의 발생확률을 반영하고 있기 때문에 발생할 확률이 많은 데이터에 대하여 네트워크가 더 잘 학습하도록 만들어 준다.
$\int_x div(f(X;W), g(X))P(X)dX \approx \frac{1}{N} \sum_i div(f(X_i; W), d_i)$ 이기 때문에 데이터 발생확률이 높을 수록 더 많은 샘플이 수집되었을 것이기 때문이다.
'Deep Learning' 카테고리의 다른 글
| Neural Networks: What can a network represent 2 (0) | 2022.11.20 |
|---|---|
| Neural Networks: What can a network represent 1 (1) | 2022.11.19 |


