| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Deep Learning
- Universal Classifier
- 시간복잡도#기본산술연산#덧셈#곱셈#나눗셈#비트연산
- parameters
- tv shows
- MLP
- Collaborative Filtering
- implicit feedback
- neural network
- 협력필터링
- FCN #Fully Convolution #Semantic Segmentation
- nn
- learning a neural network
- 인공신경망 학습
- latent factor model
- perceptron
- 알고리즘#수행시간#BigO
- Today
- Total
Study
Neural Networks: What can a network represent 1 본문
This is a summary of 11-785 2022 Fall at CMU.

딥러닝은 입력을 받아서 출력을 만들어내는 함수(black box) 이다. 우리의 목표는 black box가 사람의 뇌를 흉내내도록 만들어서 원하는 task를 해결하는 것이다. 따라서, 딥러닝은 사람의 뇌의 네트워크 구조(a network of neurons)를 모방하도록 만들어진다.
뉴런은 서로 다른 가중치를 갖는 여러 신호가 입력으로 들어와서, 이 신호들의 가중합이 임계치를 넘어서면 활성화되고 그렇지 않으면 활성화되지 않는 뇌의 기본 단위(unit)이다. 각각의 뉴런들은 아주 단순한 기본 단위이지만, 이들이 어떻게 연결되는지에 따라 다양하고 복잡한 역할을 수행할 수 있다.
그리고 인공신경망은 인간 뇌의 뉴런에 대응되는 퍼셉트론의 네트워크들로 구성되어 있다(Neural networks are composed of networks of computational models of neurons called perceptrons).

하나의 퍼셉트론은 여러 입력을 받으며, 각각의 입력은 대응되는 가중치를 가진다. 입력에 대응되는 가중치를 곱한 것들의 합이 퍼셉트론의 임계치를 넘으면 해당 퍼셉트론은 활성화가 되고, 그렇지않으면 활성화되지 않는다. 여기서 입력들의 가중합에 임계치를 적용하는 연산은 affine 연산으로 대체될 수 있으며, affine 연산의 결과가 양수가 되면 해당 퍼셉트론이 활성화된다.

affine 연산과 linear 연산의 차이는 상수항의 유무이다. 즉, affine 연산에서 상수항이 0인 경우를 linear 연산이라고 한다. linear 연산의 결과는 원점을 지나는 hyperplane인 반면에 affine 연산의 결과는 공간의 어디로든 shift될 수 있다는 차이점이 있다.
linear 연산 + 임계값 비교 대신에 affine 연산으로 대체하게 되면, affine 연산 뒤의 activation 함수를 맘대로 바꿀 수 있게 되는(flexibility 증가) 장점이 있다.
* activation 함수의 종류: sigmoid, ReLu, Tanh, ...

다층 퍼셉트론은 기본적으로 퍼셉트론들의 네트워크이다. 다층 퍼셉트론에서는 퍼셉트론들의 출력이 다시 다른 퍼셉트론들의 입력이 된다.
Deep neural network에서 deep의 의미는 무엇일까?
네트워크의 깊이(depth)가 깊은 것을 의미한다.

그렇다면 네트워크의 깊이는 어떻게 정의될까?
방향성 그래프에서 source 노드에서 sink 노드까지의 경로들 중에서 가장 긴 경로의 길이를 그래프의 깊이라고 한다.
neural network 역시 방향성 그래프이다. 네트워크의 입력을 받는 노드가 source이고, 네트워크의 출력을 담당하는 노드가 sink라고 할 수 있다.
"deep"하다는 것은 네트워크의 depth가 2보다 큰 것을 말한다.

그렇다면 layer는 무엇인가?
방향성그래프의 sink에서 동일한 깊이만큼 떨어져 있는 노드들(혹은 neural network에서 입력에서부터 동일한 깊이만큼 떨어져있는 퍼셉트론들)의 집합을 layer라고 부른다.
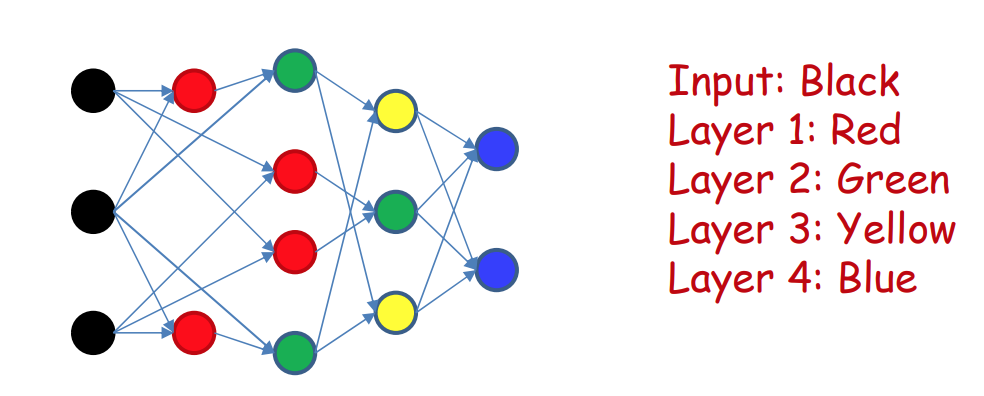
(Remark: depth는 입력노드로부터의 경로 중 가장 긴 경로의 길이로 정의됨)
다층 퍼셉트론은 boolean function을 구성할 수 있으며, 실수 함수(real-valued function)를 구성할 수도 있다.

기본적으로 단일 퍼셉트론은 binary boolean gates(and, not, or 등)를 표현할 수 있다.

입력 $X_i$가 0 또는 1의 값을 가진다고 했을 때, 임계값이 $L$이고 $X_i$에 대한 가중치가 $1 \leq i \leq L$의 범위에서 1이고 $L+1 \leq i \leq N$의 범위에서 -1인 퍼셉트론은 $X_i$가 $1 \leq i \leq L$의 범위에서 1이면서 동시에 $L+1 \leq i \leq N$ 의 범위에서 0이어야만 활성화된다.
이처럼 퍼셉트론은 보편적인 AND 게이트를 표현할 수 있다.

입력 $X_i$가 0 또는 1의 값을 가진다고 했을 때, 임계값이 $L-N+1$이고 $X_i$에 대한 가중치가 $1 \leq i \leq L$의 범위에서 1이고 $L+1 \leq i \leq N$의 범위에서 -1인 퍼셉트론은 $1 \leq i \leq L$의 범위에서 $X_i=0$ 이고 $L+1 \leq i \leq N$ 의 범위에서 $X_i=1$이면 이들의 가중합은 $L-N$이 된다.
따라서, $1 \leq i \leq L$ 의 범위의 $X_i$가 어느 하나라도 1의 값을 가지거나, $L+1 \leq i \leq N$ 의 범위에서 $X_i$가 어느 하나라도 0의 값을 가지게 되면 그들의 가중합은 $L-N+1$보다 크거나 같게 되므로 퍼셉트론은 활성화된다.
이처럼 퍼셉트론은 보편적인 OR 게이트도 표현가능하다.

모든 입력에 대한 가중치를 1로 부여하고, 임계값을 $입력의 개수/2$로 설정하면 majority 게이트도 표현 가능하다.
하지만 단일 퍼셉트론으로는 XOR 게이트는 표현이 불가능하며, XOR 게이트를 표현하기 위해서는 다층 퍼셉트론(MLP)이 필요하다. 3개의 퍼셉트론 또는 2개의 퍼셉트론으로도 XOR 게이트를 표현할 수 있지만, 어쨌든 layer가 2 이상이어야 가능하다.
 |
 |
이렇듯 다층 퍼셉트론은 AND, OR, majority, 그리고 XOR 게이트까지 모든 게이트들을 표현할 수 있으므로 다층 퍼셉트론은 universal boolean function이라고 할 수 있다. 즉, 어떠한 boolean function이 주어지더라도 이를 다층 퍼셉트론으로 표현하는 것이 가능하다.

그렇다면 어떤 임의의 boolean function이 주어졌을 때, 이를 표현하기 위해 필요한 최소 layer의 수는 몇일까? 정답은 2이다.
Boolean function은 결국 진리표(truth table)와 동일한 기능을 수행한다. 진리표에서 결과값이 1이 나올 수 있는 입력의 조합을 1층(은닉층)에서 표현한 후에 이들의 OR연산을 하면 진리표의 내용을 모두 표현 가능해지기 때문이다.
따라서 하나의 은닉층을 갖는 다층퍼셉트론은 universal boolean function이다.
하지만 진리표를 1개의 은닉층을 갖는 MLP로 표현하기 위해서는 입력 변수의 exponential 개수만큼의 퍼셉트론이 사용되어야 한다.
그러면 더 적은 개수의 퍼셉트론만 사용해서 함축적으로 표현할 수는 없을까?

왼쪽 karnaugh map에서 행은 변수 $W$와 $X$의 서로 다른 조합들(00, 01, 11, 10)을 나타내며, 열은 변수 $Y$와 $Z$의 서로 다른 조합들(00, 01, 11, 10)을 나타낸다.
인접한 두 셀에 대응되는 값들은 서로 한 비트를 차이가 난다.
( 예: (1,1) = 0101 / (1,2)=0111 )
map의 가장 왼쪽 셀들((0,0), (1,0), (2,0), (3,0))과 가장 오른쪽 셀들((0,3), (1,3), (2,3), (3,3))도 서로 한 비트 차이이며, 윗쪽 끝 셀들((0,0), (0,1), (0,2), (0,3))과 아래쪽 끝 셀들((3,0), (3,1), (3,2), (3,3))도 서로 한 비트 차이이다. 따라서 karnaugh map은 2차원 표로 표현되어 있지만 사실은 실린더모양이라고 생각할 수 있다.
karnaugh map에서 노란색으로 칠해진 칸들이 출력 값이 1인 입력의 조합이라고 해보자. 현재의 예시에서는 변수 $W$, $X$, $Y$, $Z$ 의 16가지 발생 가능한 모든 입력의 조합 중에서 7개의 조합에 대한 출력이 1이다. 이제 노란 칸들을 grouping해보자.

빨간색으로 묶인 덩어리(map에서 첫번째 열)는 $W$와 $X$의 값에 상관없이 $Y$와 $Z$가 0의 값을 가지면 무조건 1을 출력한다.
이와 유사하게 초록색으로 묶인 덩어리는 $Z$의 값에 상관없이 $W$와 $Y$가 0가 0이고 $X$가 1이면 1을 출력한다.
그리고 검은색으로 묶인 덩어리는 $W$의 값에 상관없이 $X$, $Z$가 0을, $Y$가 1의 값을 가지면 1을 출력한다.
이렇듯 grouping을 통해서 DNF를 조금 더 간단하게 표현할 수 있고, 다층 퍼셉트론도 더 컴펙트하게 표현가능해진다.

하지만 karnaugh map이 chess board 모양인 경우, grouping할 수 없어서 축약적 표현이 불가능하다.
이 경우 만약에 하나의 은닉층만 가지는 MLP인 경우, 은닉층에 $2^{(N-1)}$개의 퍼셉트론이 필요하다. 각 변수마다 0 또는 1의 값을 가질 수 있고 변수의 개수는 $N$이므로 총 $2^N$가지의 조합이 존재하는데, 이 중에서 1의 값을 가지는 조합은 반절이므로 $2^N/2 = 2^{(N-1)}$ 이기 때문이다.

chess board모양은 네 변수의 XOR 연산(W⊕X⊕Y⊕Z) 으로 표현 가능하다. 예를 들어 W=0, X=1, Y=0, Z=0이면, W⊕X=1 --> (W⊕X)⊕Y=(1⊕0)=1 --> ((W⊕X)⊕Y)⊕Z=(1⊕0)=1
하나의 XOR은 3개의 퍼셉트론으로 표현 가능하며, 네 변수의 XOR연산은 3개의 XOR로 표현되므로, 총 $3*3=9(=3*N-1)$개의 퍼셉트론으로 4x4 chess board를 표현할 수 있다.
따라서 하나의 은닉층으로 boolean function을 표현할 때 exponential 개수의 퍼셉트론이 필요했던 데에 비해, 여러 은닉층(깊은 네트워크)로 boolean function을 표현할 때는 linear 개수의 퍼셉트론만 필요하므로, 깊은 네트워크로 boolean function을 표현하면 더 효율적이다.

그러면 네트워크는 얼마나 깊어야 할까?
XOR 연산은 associative하다. (associative: rearranging the parentheses in an expression will not change the result) -> 2개씩 pair로 짝찌었을 때, $\log N$개의 layers로 boolean function을 표현할 수 있다.

만약에 k개의 layers만 사용할 수 있다면, boolean function을 완벽하게 표현하기 위해 필요한 퍼셉트론은 몇개일까?
출력을 위한 마지막 layer를 제외하면 사용할 수 있는 layers의 개수는 총 $k-1$개이다. 이 때, XOR 연산을 표현하기 위해서는 2개의 layers가 사용되고, 한번 XOR연산을 거칠 때마다 2개의 변수가 서로 grouping되어 하나로 합쳐지므로, 2개의 layers를 지날 때마다 퍼셉트론의 개수는 반절로 줄어든다. 따라서, $k-1$개의 layers를 거친 이후에 남은 퍼셉트론의 개수는 $N*(1/2)^{(k-1)/2}$ 이고, 각 변수는 두 종류의 값을 가지므로 boolean function을 온전히 표현하기 위해 마지막 $k$번째 layer에서 필요로하는 노드의 개수는 총 $O(2^{N*(1/2)^{(k-1)/2}})$이다.

단일 은닉층을 갖는 네트워크든지 깊은 네트워크든지 상관없이 MLP는 모두 universal boolean machine이지만, 네트워크의 깊이에 따라 필요로 하는 퍼셉트론(뉴런)의 개수가 달라진다.

한 발자국 더 나아가, 네트워크의 입력이 boolean값이 아닌 실수값으로 주어지고 출력이 범주성 값이나 boolean 값인 경우, 그러한 네트워크를 분류기(classifier) 라고 부른다.
다층 퍼셉트론(MLP)는 실수공간에서 복잡한 결정경계를 찾는 함수라고도 할 수 있다.

퍼셉트론의 입력이 실수값인 경우, 입력들의 가중합이 임계값을 넘어가면 해당 퍼셉트론의 출력은 1, 그렇지않으면 0이 된다.
이렇게 동작하는 단일 퍼셉트론은 선형 분류기(linear classifier)로 볼 수도 있다.

실수 뿐만 아니라 boolean을 입력으로 받는 퍼셉트론 역시 선형 분류기이다.
오른쪽 예시에서 보라색 영역에 속하는 영역의 출력은 1이 되고, 그러한 영역을 정의하는 검은 실선이 하나의 퍼셉트론이다.
세번째 예시는 XOR을 나타내고 있으며, 하나의 퍼셉트론만으로는 표현 불가능하며 최소 2개 이상의 퍼셉트론이 필요하다.
'Deep Learning' 카테고리의 다른 글
| Neural Networks Learning the network: Part 1 (0) | 2023.01.01 |
|---|---|
| Neural Networks: What can a network represent 2 (0) | 2022.11.20 |


