| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 인공신경망 학습
- 협력필터링
- tv shows
- nn
- latent factor model
- implicit feedback
- learning a neural network
- MLP
- 알고리즘#수행시간#BigO
- Collaborative Filtering
- 시간복잡도#기본산술연산#덧셈#곱셈#나눗셈#비트연산
- FCN #Fully Convolution #Semantic Segmentation
- parameters
- neural network
- Deep Learning
- Universal Classifier
- perceptron
- Today
- Total
Study
Neural Networks: What can a network represent 2 본문
This is a summary of 11-785 2022 Fall at CMU.

MLP(multi-layer perceptron)로 복잡한 결정경계도 표현 가능하다.
좌측의 오각형을 MLP로 표현하기 위해서는, 퍼셉트론 한 개마다 오각형의 변 하나를 나타내도록 한 뒤 AND 연산을 담당하는 퍼셉트론을 하나 더 사용하면 된다.
모든 convex polygon은 polygon의 변의 개수만큼 퍼셉트론을 사용하여 변들을 표현한 뒤 AND 연산을 담당하는 퍼셉트론을 하나 더 사용하여 표현 가능하다.
그렇다면 여러개의 convex polygons들이 이루는 결정경계는 어떻게 표현할 수 있을까?

각각의 polygon들을 나타내는 퍼셉트론을 OR 연산을 수행하는 퍼셉트론으로 연결함으로써 표현 가능하다.
그렇다면 각각의 polygon이 convex하지 않다면 어떻게 표현할 수 있을까?
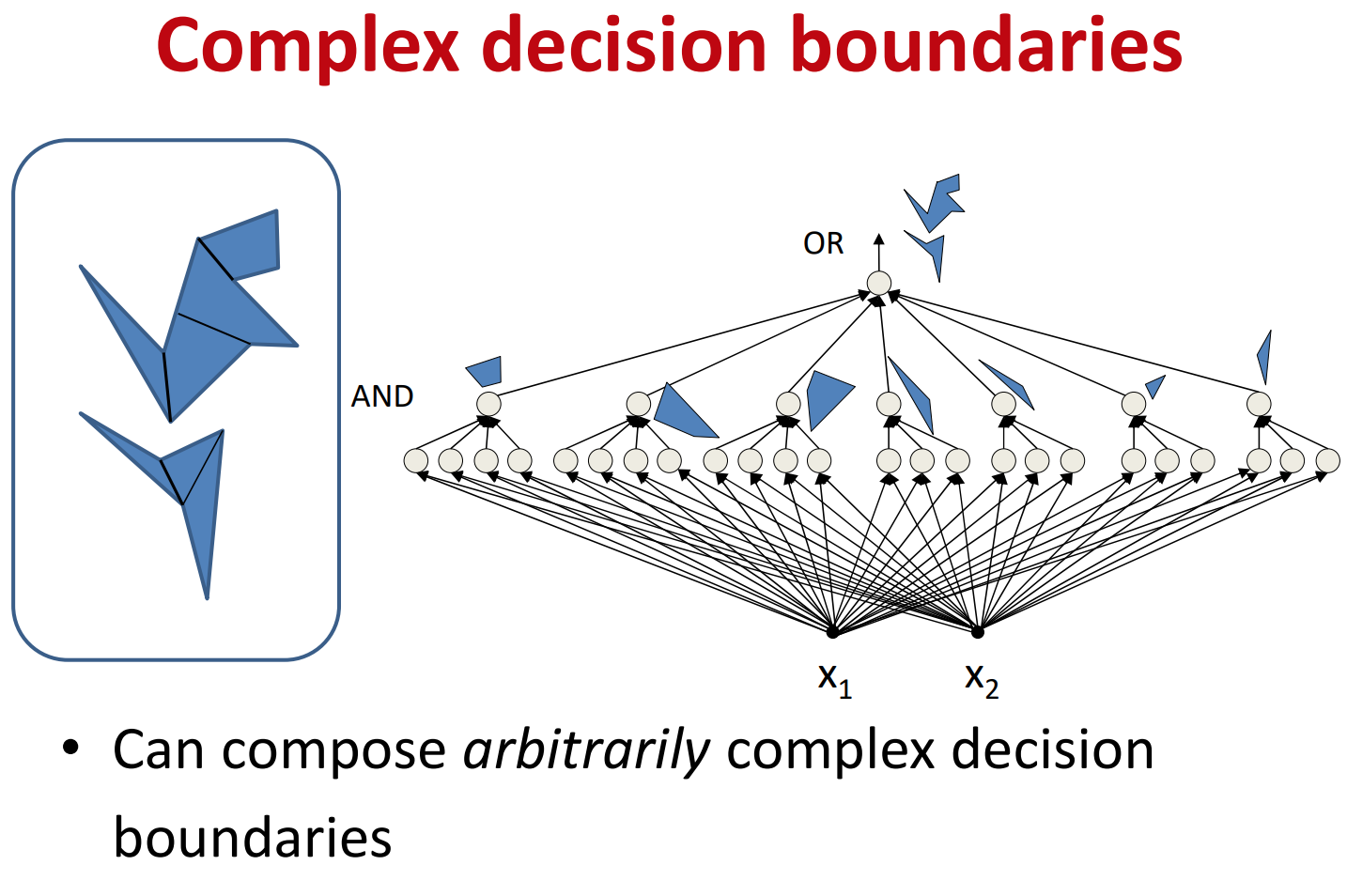
convex 하지 않은 polygon은 여러개의 convex polygons로 나누어서 표현하면 된다.
그 후 convex polygons들을 OR로 연결하면 표현하고싶은 결정경계가 얼마나 복잡하든 상관없이 표현 가능하다.

그렇다면 여러 개의 convex polygon들로 구성된 결정경계를 하나의 은닉층만을 사용하여 표현하는 방법은 없을까?

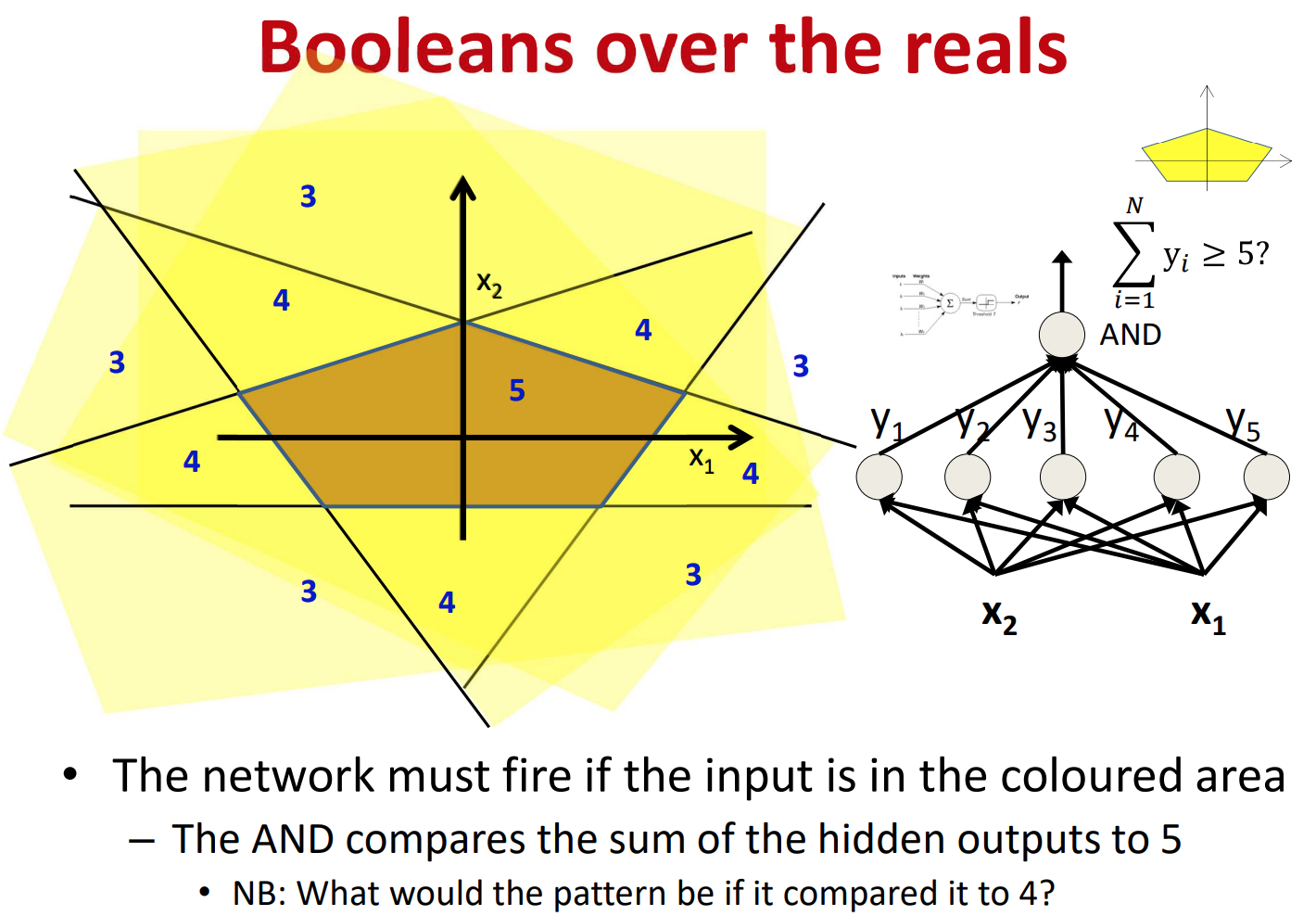
사각형 모양의 결정경계는 다음과같이 4개의 퍼셉트론으로 네 변을 표현한 뒤 네 개의 퍼셉트론의 출력의 합이 임계값(=4)을 넘는지의 여부로 표현할 수 있다.
이 때, 4각형의 주변을 살펴보면, 사각형의 각 변과 접하고 있는 열린영역(노란색 영역)은 네 개의 퍼셉트론의 출력의 합이 3(임계값보다 1 모자른 값)인 것을 확인 할 수 있으며, 흰 색으로 표시된 영역은 네 개의 퍼셉트론의 출력의 합이 2인 것을 확인할 수 있다.
(임계값을 3차원 그림으로 표현하면 결정경계 내부가 가장 높게 나타나는것을 확인할 수 있다.)

오각형 모양의 결정경계도 사각형 모양과 마찬가지로, 변의 개수만큼의 퍼셉트론을 사용하여 각 변을 표현한 뒤, 해당 퍼셉트론들의 출력의 합이 임계값을 넘는지의 여부로 표현할 수 있다.
그리고 결정경계의 주변 영역들의 값들을 살펴보면, 결정경계와 가장 가까운 영역에서부터 점차 먼 영역들로 갈 수록 퍼셉트론들의 출력의 합이 작아지는 것을 확인할 수 있다.
(임계값을 3차원 그림으로 표현하면 결정경계 내부가 사각형보다 더 높게 나타나는것을 확인할 수 있다.)

변의 개수가 점점 많아지면 어떻게 될까?
가운데가 점점 더 솟아오르는 형태로 3차원 그래프가 그려지게 된다.

결정경계를 구성하는 다각형의 변의 개수가 많으면 많을 수록 결정경계의 내부와 외부 사이의 높이는 현격하게 차이난다.

왜냐하면 변의 개수의 증가가 결정경계의 외부영역 중에서 퍼셉트론의 출력의 합이 $N/2 < \sum(y_i) < N$ 인 영역을 점점 감소시키기 때문이다.

변의 개수를 무한히 크게하면,
결정경계의 바깥 영역은 $N/2$의 값을 갖고 내부 영역은 $N$의 값을 갖는 거의 실린더에 가까운 형태가 된다.

따라서 좌표평면에서 원 모양의 결정경계는 매우 많은 수의 퍼셉트론을 사용하여 표현 가능하며, 결정경계의 내부는 퍼셉트론의 출력의 합이 $N$, 그리고 결정경계의 외부는 거의 모든 영역에서 퍼셉트론의 출력의 합이 $N/2$으로 나타난다.
이러한 원들은 좌표평면의 어디든 위치시킬 수 있다.

이 때, $-N/2$를 편향값으로 더해주는 퍼셉트론을 하나 추가하면 결정경계의 외부 영역은 거의 대체로 0의 값을 갖게 된다.
이렇게 추가 퍼셉트론을 통해 편향항까지 반영해주면, 네트워크를 구성하는 모든 퍼셉트론들의 합이 0보다 큰 값을 갖는 경우, 입력으로 들어온 좌표는 원의 내부 영역에 속하는 점이라고 할 수 있다.

좌표평면의 어느 위치든지 원을 위치시킬 수 있고, 이런 방식으로 여러개의 원을 동시에 위치시키는 것도 가능하다.
각 원을 나타내는 서브 네트워크들을 더해서(concatenate) 만든 하나의 큰 네트워크를 생각해보자. 그 네트워크의 은닉층에 속한 퍼셉트론들의 출력의 합이 $N/2$라면, 네트워크가 표현하는 여러 원들 중 어느 하나의 원 내부에 입력으로 들어온 점이 속하는 것을 의미한다.
한편, 어떤 원의 내부에도 속하지 않은 점이 네트워크의 입력으로 주어진 경우 그 출력값은 거의 0을 갖게 된다.

따라서 임의의 개수의 원들을 사용하여 여러 개의 convex polygon으로 구성되어있는 영역을 꽉 채우는 식으로 해당 영역을 표현하는 것이 가능하다.
이 때, 큰 사이즈의 원을 적은 개수로 사용하는 것보다는 작은 사이즈의 원을 많이 사용하여 영역을 채우면 더 정확한 근사가 가능해진다.
기본적으로 다층퍼셉트론(MLP)는 어떠한 모양을 갖는 결정경계든 전부 표현 가능하며, 꼭 MLP가 여러 개의 층으로 구성되어 있지 않더라도 (하나의 은닉층만을 가지는 MLP이더라도) 복잡한 결정경계를 표현할 수 있다.
따라서 MLP는 어떤 분류문제든 그 문제를 푸는데 필요한 결정경계를 모두 표현 가능한 universal classifier이다.

은닉층이 한 개인 MLP도 다양한 결정경계를 표현할 수 있지만, 네트워크의 깊이를 깊게 만들면(더 많은 개수의 은닉층을 사용하면) 은닉층이 한 개인 MLP에 비해서 훨씬 적은 개수의 퍼셉트론만 사용해서 원하는 결정경계를 표현할 수 있게 된다.

그렇다면 네트워크의 최적 깊이는 어떻게 알 수 있을까?
네트워크의 최적 깊이와 크기에 관한 분석은 여전히 연구대상이다.

일반적인 네트워크가 표현해야하는 최악의 경우의 결정경계를 생각해보자.
은닉층이 한 개인 MLP로 왼쪽의 결정경계(체스보드)를 표현하기 위해서는 무수히 많은 수의 퍼셉트론을 필요로 할 것이다.

하나가 아니라 두 개의 은닉층을 사용하여 동일한 결정경계를 표현하는 경우,
네트워크의 1층에서는 기초적으로 결정경계를 구성하는 변(빨간 선)을 표현하고 2층에서는 1층에서 표현된 변들을 활용하여 표현하고 싶은 각각의 영역(노란 영역)을 표현한 후에 3층에서 이들의 합이 임계값을 넘는지 확인함으로써 네트워크의 입력이 여러 영역 중 어느 한 영역에 포함되는지 확인할 수 있다.

이를 위해 네트워크의 첫번째 은닉층에서는 결정경계를 이루는 변의 개수와 동일한 개수의 퍼셉트론(16개)을 사용하고,
이 변들을 활용하여 2층에서는 노란색 영역의 개수(40개)만큼 퍼셉트론을 사용하여 각 영역을 표현한 후에,
출력층에서는 2층 퍼셉트론들의 출력의 합이 임계값을 넘는지 계산하는 퍼셉트론를 하나 사용하면 된다.

하지만 체스보드는 결국 결정경계를 이루는 변들의 XOR연산으로 표현이 가능하기 때문에, 첫번째 은닉층의 출력에 대하여 XOR연산을 수행함으로써 표현 가능하다.
16개의 퍼셉트론의 출력($Y_1, ..., Y_{16}$)에 대하여 2개의 퍼셉트론씩 쌍을지어 XOR연산을 시키면,
(XOR연산기준으로 층을 셌을 때) XOR 1층에서는 8쌍, XOR 2층에서는 4쌍, XOR 3층에서는 2쌍, XOR 4층에서 1쌍에 대하여 XOR연산을 하게 된다.
XOR 연산 한 번에는 3개의 퍼셉트론이 필요하며 총 15쌍에 대하여 XOR 연산을 수행하므로, 이 네트워크에서 필요한 퍼셉트론의 수는 처음 16개의 경계선을 표현하는 퍼셉트론 16개+XOR연산 15쌍*퍼셉트론 3개 = 총 61개이다.
체스보드가 더 빽빽해지면 필요한 퍼셉트론의 수는 어떻게 변할까?

이번에는 체스보드를 구성하는 변의 개수가 64개인 경우를 살펴보자.
(이전 예시 16개의 변 -> 현재 예시 64개)

2개의 은닉층을 사용하여 네트워크를 구성했을 때 필요한 퍼셉트론의 수는 609개이다.
[ 층별 필요한 퍼셉트론의 수 ]
은닉층 1층: 경계선의 개수(=64개)
은닉층 2층: 표현하고자하는 영역(노란영역)의 개수(=544개)
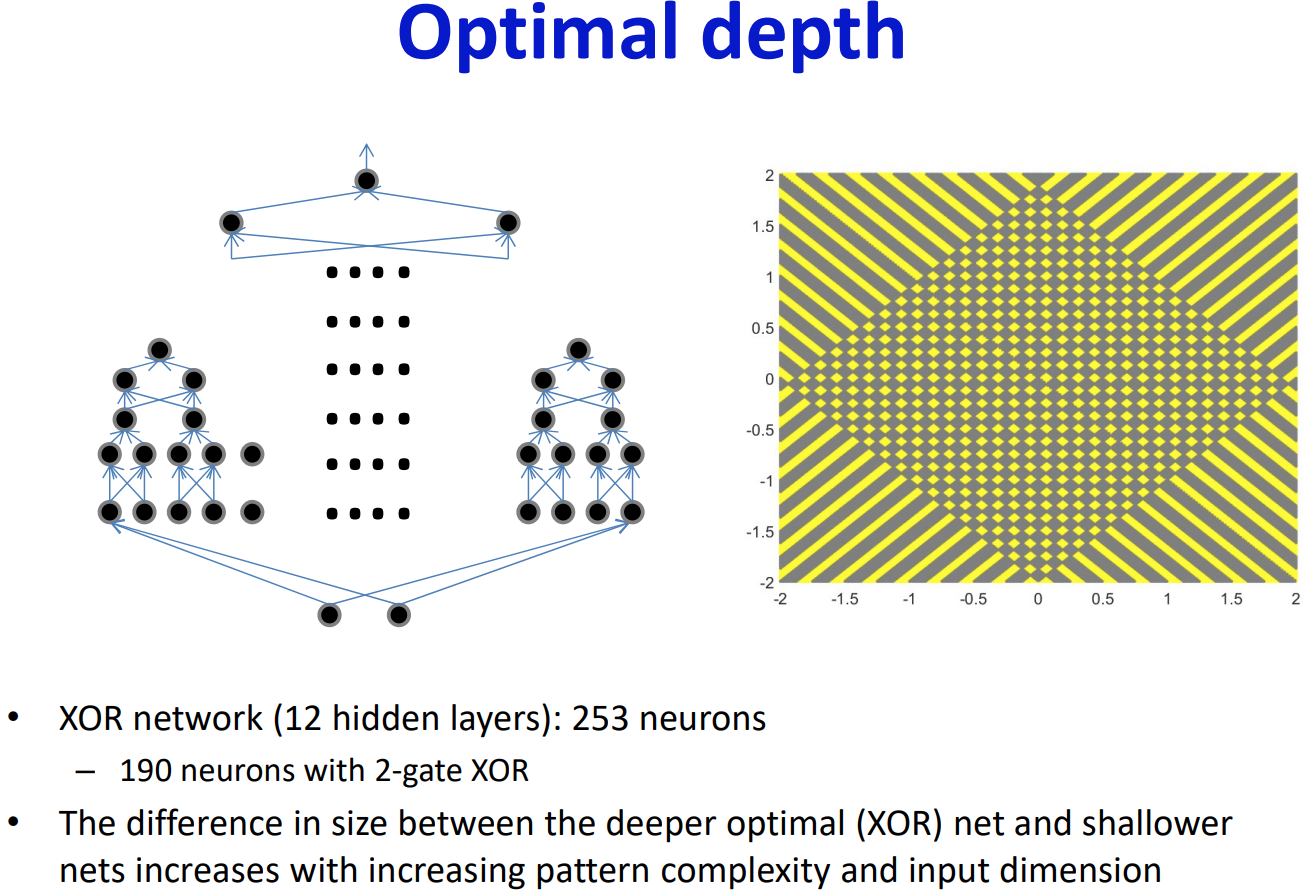
동일한 체스보드를 XOR연산을 하는 네트워크로 표현했을 때 필요한 퍼셉트론의 수는 253개이다.
은닉층 1층: 경계선의 개수(=64개)
XOR 1층: 은닉층 1층의 절반(=32개)*3개 = 64개
XOR 2층: XOR 1층의 절반(=16개)*3개 = 48개
... 마지막 출력층: XOR 1쌍*3개 = 3개
--> 총 XOR층의 개수 = $\log_2 32$ = 5층
표현하고자하는 체스보드의 결정경계를 이루는 경계선의 개수가 많으면 많을수록 XOR로 표현하는 것이 이득이다.
XOR로 표현하는 경우 그 네트워크의 깊이는 $\log$ 경계선 수 이다.

XOR이 아니라 은닉층 2개로 네트워크를 구성하더라도 여전히 필요한 퍼셉트론의 수는 결정경계를 이루는 경계선 개수를 N이라고 했을 때 N의 제곱 만큼만 필요로한다.
그럼 왜 굳이 XOR로 패턴을 표현해야 할까?
우리가 살펴본 예시는 입력이 2차원일 때를 가정하고 있다. 하지만 입력이 2차원이 아닌 경우는 문제가 달라진다.
왜냐하면, 패턴을 표현하기 위해 필요로하는 퍼셉트론의 수는 입력 차원의 지수배만큼 증가하게 되어있기 때문이다.
따라서 얕은 네트워크를 사용하여 고차원의 데이터에 대한 복잡한 결정경계를 형성해야 하는 경우, 경우에 따라 다르겠지만, 최악의 경우 네트워크에서 필요로하는 퍼셉트론의 수를 지수배만큼 증가시킬 수 있다.
하지만 XOR로 네트워크를 형성하게 되면 첫번째 은닉층의 퍼셉트론의 사이즈에만 영향을 받게 되기 때문에(결정경계가 표현하고자 하는 영역의 개수에는 영향을 받지 않음) 훨씬 적은 수의 퍼셉트론만을 사용해서 동일한 결정경계를 표현할 수 있게 된다.
'Deep Learning' 카테고리의 다른 글
| Neural Networks Learning the network: Part 1 (0) | 2023.01.01 |
|---|---|
| Neural Networks: What can a network represent 1 (1) | 2022.11.19 |


