| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 시간복잡도#기본산술연산#덧셈#곱셈#나눗셈#비트연산
- Collaborative Filtering
- 협력필터링
- Universal Classifier
- neural network
- parameters
- perceptron
- FCN #Fully Convolution #Semantic Segmentation
- MLP
- latent factor model
- nn
- learning a neural network
- 알고리즘#수행시간#BigO
- Deep Learning
- tv shows
- implicit feedback
- 인공신경망 학습
- Today
- Total
Study
기본적인 산술연산의 시간복잡도(비트 단위 연산) 본문

1. 덧셈
기본 속성: 세 개의 한 자릿수를 더하면 최대 두 자릿수를 넘을 수 없다.
검증: 가장 큰 한 자릿수는 9 이다. 9를 세 번 더하면 -> 9 + 9 + 9 = 27 이므로 두 자릿수이다.
(이 규칙은 십진수 외에도 기수가 2 이상인 모든 진법들에서도 만족한다.)
기본 속성을 활용하여 두 숫자의 덧셈을 하는 방법은 다음과 같다.
① 숫자들을 오른쪽 끝이 일치하도록 나열한다.
② 오른쪽에서부터 왼쪽으로 덧셈을 한다.
③ 덧셈의 합이 기수(십진수에서는 10, 이진수에서는 2)보다 크거나 같아지면 다음 왼쪽 자리로 넘긴다. (오른쪽에서 왼쪽으로 넘어온 수 = carry)
가장 오른쪽에서 시작된 최초의 덧셈은 두 개의 한자릿수끼리의 덧셈이므로 그 값은 최대 두 자릿수이다.
그 다음 덧셈들은 방법3. 에 의해 넘어온 수(carry)가 있더라도 최대 세 개의 한자릿수끼리의 덧셈이기 때문에 왼쪽으로 넘어가는 수는 항상 한 자리이다.
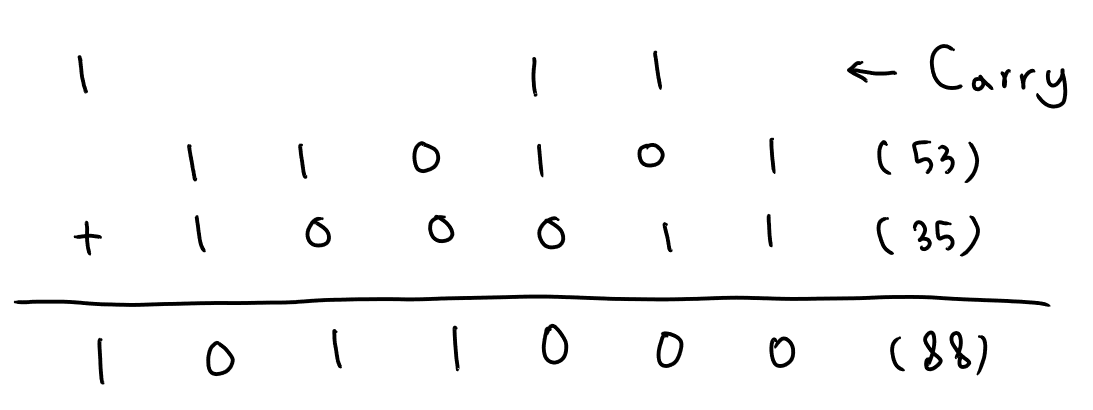
위의 예시는 53+35를 이진수의 덧셈으로 나타낸 것이다.
예시에서 확인할 수 있듯이, carry는 최대 한 자리이며, 따라서 각 자릿수에서의 합은 세 개의 한 자리 수의 합과 같다.
이렇듯 두 수의 덧셈은 각 자릿수에서 2~3개의 한 자릿수의 덧셈을 더하고자 하는 숫자들의 길이만큼 반복함으로써 수행 가능하다.(위의 예시에서는 53=110101=길이6, 35=100011=길이6 --> 6번의 한자릿수 덧셈 반복)
따라서, 두 개의 n 비트짜리 이진수가 주어졌을 때 두 수를 더하는 알고리즘의 시간복잡도는 $ O(n) $이다.
2. 곱셈
[방법 1]
예로 13*11에 대해 살펴보자.

먼저, 11과 13을 이진수로 바꾸면 각각 1011(11), 1101(13)이다.
두 이진수를 곱하는 과정은 다음과 같다.
① 13에 11의 각 자릿수 숫자를 곱한다.
② 곱셈의 각 결과를 11의 자릿수만큼 왼쪽으로 이동시켜 위부터 아래로 늘어놓는다.
③ 늘어놓은 숫자들을 더한다.

이제 n 자리 두 수 X와 Y의 곱셈으로 일반화 해보자.
위와 동일한 과정으로 곱셈을 하면 중간값이 n 개 생긴다.
(13*11의 경우 11이 이진수로 변환하면 1011(4자리)이므로 중간값이 4개 생김)
중간값은 자릿수만큼 왼쪽으로 이동하기 때문에 길이는 최대 2n이다. (13*11의 경우 n=4, 최대길이 7)
앞서 살펴봤듯이, n비트짜리 두 수의 덧셈의 시간복잡도는 $ O(n) $인데,
n개의 중간값을 모두 더하기 위해서는 덧셈을 총 n-1번 반복해야 하므로
X와 Y의 곱셈의 시간복잡도는 $ (n-1) * O(n) = O(n^2) $이다.
[방법 2]
① 두 십진수를 나란히 쓴다.
② 왼쪽 숫자를 2로 나누고 나머지는 버린다. 오른쪽 숫자는 2를 곱한다.
③ 왼쪽 숫자가 1이 될 때까지 ②번 과정을 반복한다.
④ 왼쪽 숫자가 홀수인 행들의 오른쪽 숫자들을 더한다.
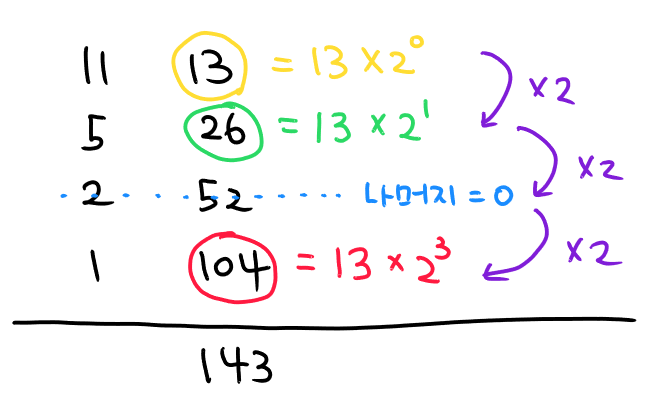
[방법 2] 도 [방법 1]과 동일하다.
다만, 십진수와 이진수를 잘 섞어서 사용했을 뿐이다.
십진수를 명시적으로 이진수로 바꾸지 않고, 대신에 2로 나누면서 나머지 유무와 자릿수만 확인하여 곱셈에 활용한다.
반복해서 2로 나누고 나머지유무를 확인하여 더해주기만 하면 되므로 [방법 2]는 재귀적으로 문제해결이 가능하다.
재귀함수 pseudo code
function multiply(x, y):
#input: 2 integers (each number is n bits)
#output: multiply 2 integers
if y == 0:
return 0
z = multiply(x, floor(y/2))
if y is even:
return 2z
else:
return x+2z
**floor는 내림함수: ex. floor(4.5) = 4
'알고리즘' 카테고리의 다른 글
| 분할정복(Divide-and-conquer) (1) | 2020.01.30 |
|---|---|
| 알고리즘 수행시간 표기법 (0) | 2020.01.09 |


